11.4 可降阶的高阶微分方程
有三种容易降阶的高阶方程：
11.4.1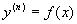 
型的微分方程
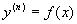（1）
方程右端只含x，容易看出，只要把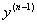
作为新的未知函数，那未（1）式就是新的未知函数的一阶微分方程。两边积分，就得到一个n-1阶的微分方程
.
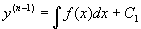同理可得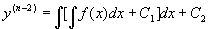 
.
依此法继续进行，接连积分n次，便得方程(1)的含有n个任意常数的通解。
例 求微分方程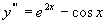
的通解
解 对所给方程接连积分三次，得
。
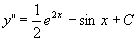
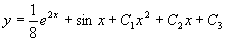
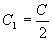这就是所求的通解。
11.4.2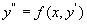 
型的微分方程
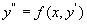（2）
方程右端不显含未知函数y，如果我们设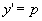
，那末
而方程就成为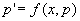
.
这是一个关于变量x, p 的一阶微分方程。设其通解为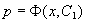
。
但是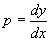
，因此又得到一个一阶微分方程
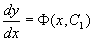
对它进行积分，便得到方程（2）的通解为
。
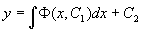例 求微分方程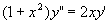
满足初始条件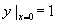
， 
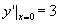
的特解。
解 所给方程是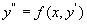型的。设y’= p，代入方程并分离变量后，有
.
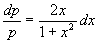两端积分，得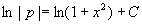 
,
即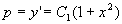 
(
),
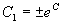由条件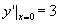，得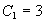
,
所以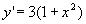
.
两端再积分，得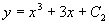 
又由条件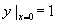，得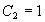 
,
于是所求的特解为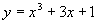
.
11.4.3 
型的微分方程
(3)
方程中不明显地含自变量x。为了求出它的解，我们令y’= p ，并利用复合函数的求导法则把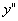
化为对y的导数，即
.
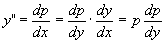这样，方程（3）就成为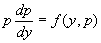
。
这是一个关于变量y, p 的一阶微分方程。设它的通解为
，
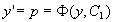分离变量并积分，便得方程（3）的通解为
。
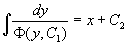例 求微分方程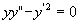 
的通解。
解 所给方程不明显地含自变量x，设
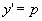, 则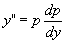
，
代入方程中，得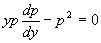
。
在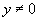
、
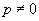时，约去p 并分离变量，得
。
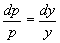两端积分，得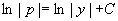
，
即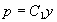 
，或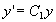 
。
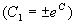再分离变量并两端积分，便得方程的通解为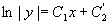
，
或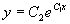 
（
）。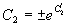