11.6 微分方程的幂级数解法
当微分方程的解不能用初等函数或其积分式表达时,我们就要寻求其它解法。常用的有幂级数解法和数值解法。本节我们简单地介绍一下微分方程的幂级数解法。
求一阶微分方程
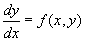 (1)
(1)
满足初始条件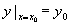 的特解,其中函数f (x , y)是
的特解,其中函数f (x , y)是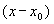 、
、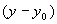 的多项式:
的多项式:
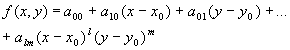 .
.
这时我们可以设所特解可展开为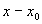 的幂级数
的幂级数
 (2)
(2)
其中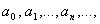 是待定的系数,把(2)代入(1)中,便得一恒等式,比较这恒等式两端
是待定的系数,把(2)代入(1)中,便得一恒等式,比较这恒等式两端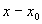 的同次幂的系数,就可定出常数
的同次幂的系数,就可定出常数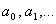 , 以这些常数为系数的级数(2)在其收敛区间内就是方程(1)满足初始条件
, 以这些常数为系数的级数(2)在其收敛区间内就是方程(1)满足初始条件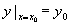 的特解。
的特解。
例1 求方程 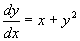 满足
满足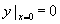 的特解。
的特解。
解 这时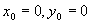 ,故设
,故设

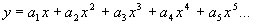 ,
,
把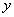 及
及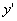 的幂级数展开式代入原方程,得
的幂级数展开式代入原方程,得
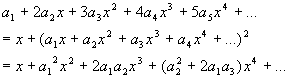
由此,比较恒等式两端x 的同次幂的系数,得
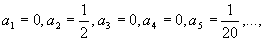
于是所求解的幂级数展开式的开始几项为
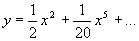 。
。
关于二阶齐次线性方程
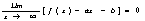 (3)
(3)
用幂级数求解的问题,我们先叙述一个定理:
定理 如果方程(3)中的系数P(x)与Q(x)可在 -R<x<R 内展开为x的幂级数那么在-R<x<R内方程(3)必有形如
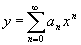
的解。
例2 求微分方程
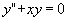
的满足初始条件
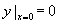 ,
, 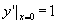
的特解。
解 这里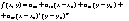 在整个数轴上满足定理的条件。因此所求的解可在整个数轴上殿开成x的幂级数
在整个数轴上满足定理的条件。因此所求的解可在整个数轴上殿开成x的幂级数
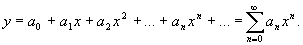 (4)
(4)
由条件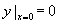 得
得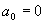 。对级数(4)逐项求导,有
。对级数(4)逐项求导,有
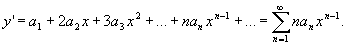 ,
,
由条件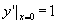 得
得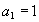 .于是我们所求方程的级数解
.于是我们所求方程的级数解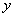 及
及 的形式已成为
的形式已成为
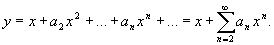 (5)
(5)
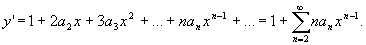 (6)
(6)
对级数(6)逐项求导,得
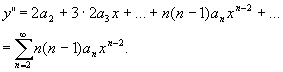 (7)
(7)
把(5)和(7)代入所给方程,并按x的升幂集项,得
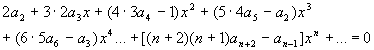
因为幂级数(4)是方程的解,上式必然是恒等式,因此方程左端各项的系数必全为零,于是有
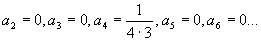
一般地 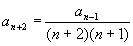 (n=3 , 4 ,…).
(n=3 , 4 ,…).
从这递推公式可以推得
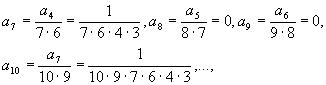
一般地
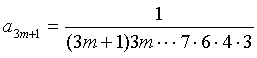 (m=1,2,…),
(m=1,2,…),
于是所求的特解为
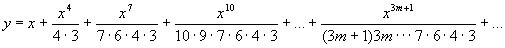 。
。
