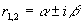11.5.1 二阶常系数齐次线形微分方程
在二阶齐次线形微分方程
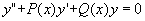 (1)
(1)
中,如果 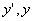 的系数P(x) ,Q(x)均为常数,即(1)式写成为
的系数P(x) ,Q(x)均为常数,即(1)式写成为
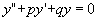 (2)
(2)
其中p,q是常数,则称(2)为二阶常系数齐次线形微分方程。如果p,q不全为常数,称(1)为二阶变系数齐次线形微分方程。
当r为常数时,指数函数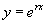 和它的各阶导数都只相差一个常数因子。由于指数函数有这个特点,因此我们用
和它的各阶导数都只相差一个常数因子。由于指数函数有这个特点,因此我们用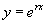 来尝试,看能否选取适当的常数r ,使
来尝试,看能否选取适当的常数r ,使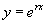 满足方程(2)。
满足方程(2)。
将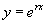 求导,得到
求导,得到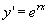
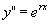
把 和
和 代入方程(2),得
代入方程(2),得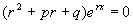
由于 ,所以
,所以
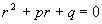 (3)
(3)
由此可见,只要r 满足代数方程(3),函数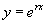 就是微分方程(2)的解。我们把代数方程(3)叫做微分方程(2)的特征方程。
就是微分方程(2)的解。我们把代数方程(3)叫做微分方程(2)的特征方程。
下面我们就通过研究特征方程(3)来研究微分方程的解。可得出求二阶常系数齐次线形微分方程
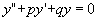 (2)
(2)
的通解的步骤如下:
第一步 写出微分方程(2)的特征方程
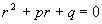 (3)
(3)
第二步 求出特征方程(3)的两个根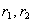 。
。
第三步 根据特征方程(3)的两个根的不同情形,按照下列表格写出微分方程(2)的通解:
特征方程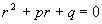 的两个根 的两个根 |
微分方程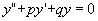 的通解 的通解 |
两个不等的实根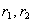
两个相等的实根
一对共轭复根 |
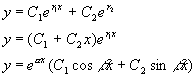 |
例1 求微分方程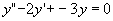 的通解。
的通解。
解 所给微分方程的特征方程为
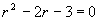
其根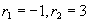 是两个不相等的实根,因此所求通解为
是两个不相等的实根,因此所求通解为
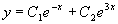
例2 求方程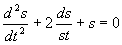 满足初始条件
满足初始条件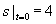 ,
,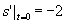 的特解。
的特解。
解 所给方程的特征方程为
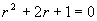
其根 是两个相等的实根,因此所求微分方程的通解为
是两个相等的实根,因此所求微分方程的通解为
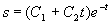
将条件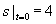 代入通解,得
代入通解,得 ,从而
,从而
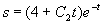
将上式对t 求导,得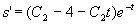 ,
,
 再把条件
再把条件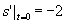 代入上式,得
代入上式,得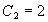 ,于是所求特解为
,于是所求特解为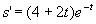 。
。
例3 求微分方程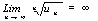 的通解。
的通解。
解 所给方程特征方程为
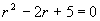
其根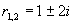 为一对共轭复根,因此所求通解为
为一对共轭复根,因此所求通解为
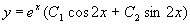 。
。
11.5.2 二阶常系数非齐次线形微分方程
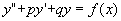 (1)
(1)
其中p,q是常数。
因为求二阶常系数非齐次线形微分方程的通解归结为求对应的齐次方程
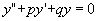 (2)
(2)
的通解和非齐次方程(1)本身的一个特解,而二阶常系数齐次线形微分方程解法已在上一知识点中讲过,所以,在此我们就只讨论方程(1)的特解。
当方程中f(x)取两种常见形式时,我们用待定系数法求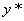 。
。
11.5.3 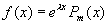 型
型
如果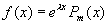 ,则二阶常系数非齐次线形微分方程(1)具有形如
,则二阶常系数非齐次线形微分方程(1)具有形如
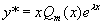 (4)
(4)
的特解,其中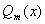 是与
是与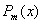 同次(m次)的多项式,而k按
同次(m次)的多项式,而k按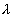 不是特征方程的根,是特征方程的单根或是特征方程的重根依次取为0,1或2。
不是特征方程的根,是特征方程的单根或是特征方程的重根依次取为0,1或2。
上述结论可推广到n阶常系数非齐次线形微分方程,但要注意(4)式中的k是特征方程含根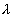 的重复次数(即若
的重复次数(即若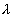 不是特征方程的根,k取为0,若
不是特征方程的根,k取为0,若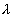 是特征方程的s重根,k取为s)
是特征方程的s重根,k取为s)
例 求微分方程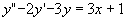 的一个特解。
的一个特解。
解 这是二阶常系数非齐次线形微分方程,且函数f(x)是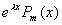 型(其中
型(其中 ,
,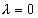 )
)
与所给方程对应的齐次方程为
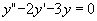
它的特征方程为

由于这里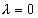 不是特征方程的根,所以应设特解为
不是特征方程的根,所以应设特解为
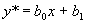
把它代入所给方程,得
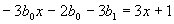
比较两端x 同次幂的系数,得
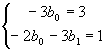
由此求得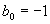 ,
, 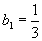 于是求得一个特解为
于是求得一个特解为
 .
.
11.5.4 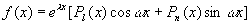 型
型
如果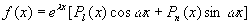 ,则二阶常系数非齐次线性微分方程(1)的特解可设为
,则二阶常系数非齐次线性微分方程(1)的特解可设为
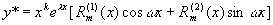 , (5)
, (5)
其中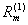 、
、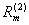 是m次多项式,m=max{l , n},而k按
是m次多项式,m=max{l , n},而k按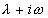 (或
(或 )不是特征方程的根、或是特征方程的单根依次取0或1。
)不是特征方程的根、或是特征方程的单根依次取0或1。
上述结论可推广到n阶常系数非齐次线性微分方程,但要注意(5)式中的k是特征方程中含根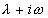 (或
(或 )的重复次数。
)的重复次数。
例 求微分方程 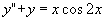 的一个特解。
的一个特解。
解 所给方程是二阶常系数非齐次线性方程,且f(x) 属于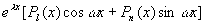 型(其中
型(其中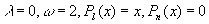 )。
)。
与所给方程对应的齐次方程为
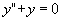 ,
,
它的特征方程为
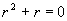 。
。
由于这里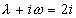 不是特征方程的根,所以应设特解为
不是特征方程的根,所以应设特解为
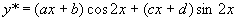 。
。
把它代入所给方程,得
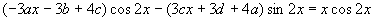 。
。
比较两端同类项的系数,得
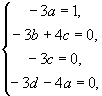
由此解得 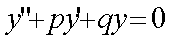 。
。
于是求得一个特解为 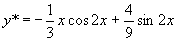 。
。