mpu6050姿态融合原理及程序代码 - 全文

　　姿态角（Euler角）pitch yaw roll

　　飞行器的姿态角并不是指哪个角度，是三个角度的统称。

　　它们是：俯仰、滚转、偏航。你可以想象是飞机围绕XYZ三个轴分别转动形成的夹角。

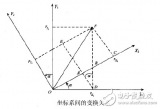
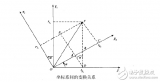
　　地面坐标系（earth-surface inertial reference frame）Sg--------OXgYgZg

　　

　　①在地面上选一点Og

　　②使Xg轴在水平面内并指向某一方向

　　③Zg轴垂直于地面并指向地心（重力方向）

　　④Yg轴在水平面内垂直于Xg轴，其指向按右手定则确定

　　机体坐标系（Aircraft-body coordinate frame）Sb-------OXYZ

　　

　　①原点O取在飞机质心处，坐标系与飞机固连

　　②x轴在飞机对称平面内并平行于飞机的设计轴线指向机头

　　③y轴垂直于飞机对称平面指向机身右方

　　④z轴在飞机对称平面内，与x轴垂直并指向机身下方

　　欧拉角/姿态角（Euler Angle）

　　

　　

　　机体坐标系与地面坐标系的关系是三个Euler角，反应了飞机相对地面的姿态。

　　俯仰角θ（pitch）：机体坐标系X轴与水平面的夹角。当X轴的正半轴位于过坐标原点的水平面之上（抬头）时，俯仰角为正，否则为负。

　　

　　偏航角ψ（yaw）：

　　机体坐标系xb轴在水平面上投影与地面坐标系xg轴（在水平面上，指向目标为正）之间的夹角，由xg轴逆时针转至机体xb的投影线时，偏航角为正，即机头右偏航为正，反之为负。

　　

　　滚转角Φ（roll）：机体坐标系zb轴与通过机体xb轴的铅垂面间的夹角，机体向右滚为正，反之为负。

　　

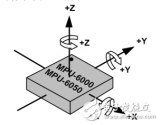
　　首先要明确，MPU6050是一款姿态传感器，使用它就是为了得到待测物体（如四轴、平衡小车）x、y、z轴的倾角（俯仰角Pitch、滚转角Roll、偏航角Yaw）。我们通过I2C读取到MPU6050的六个数据（三轴加速度AD值、三轴角速度AD值）经过姿态融合后就可以得到Pitch、Roll、Yaw角。

　　主要介绍三种姿态融合算法：四元数法、一阶互补算法和卡尔曼滤波算法。

　　一、四元数法

　　关于四元数的一些概念和计算就不写上来了，我也不懂。我能告诉你的是：通过下面的算法，可以把六个数据转化成四元数（q0、q1、q2、q3），然后四元数转化成欧拉角（P、R、Y角）。

　　虽然MPU6050自带的DMP库可以直接输出四元数，减轻STM32的运算负担，这里在此没有使用，因为我是用STM32的硬件I2C读取MPU6050数据的，DMP库需要对I2C函数进行修改，如DMP库中的I2C写：i2c_write（st.hw-》addr，st.reg-》pwr_mgmt_1，1，&（data［0］））；有4个输入变量，而STM32硬件I2C的I2C写为：voidMPU6050_I2C_ByteWrite（u8slaveAddr，u8pBuffer，u8writeAddr），只有3个输入量（这之间的差异好像是由于MPU6050的DMP库是针对MSP430单片机写的），所以必须进行修改，但是改固件库是一件很痛苦的事，你们应该都懂。当然，如果你用模拟I2C的话，是容易实现的，网上的DMP移植几乎都是基于模拟I2C的。

　　要注意的的是，四元数算法输出的是三个量Pitch、Roll和Yaw，运算量很大。而像平衡小车这样的例子只需要一个角（Pitch或Roll）就可以满足工作要求，个人觉得做平衡小车最好不用四元数法。

　　#include《math.h》

　　#include“stm32f10x.h”

　　//------------------------

　　//变量定义

　　#defineKp100.0f//比例增益支配率收敛到加速度计/磁强计

　　#defineKi0.002f//积分增益支配率的陀螺仪偏见的衔接

　　#definehalfT0.001f//采样周期的一半

　　floatq0=1，q1=0，q2=0，q3=0;//四元数的元素，代表估计方向

　　floatexInt=0，eyInt=0，ezInt=0;//按比例缩小积分误差

　　floatYaw，Pitch，Roll;//偏航角，俯仰角，翻滚角

　　voidIMUupdate（floatgx，floatgy，floatgz，floatax，floatay，floataz）

　　{

　　floatnorm;

　　floatvx，vy，vz;

　　floatex，ey，ez;

　　//测量正常化

　　norm=sqrt（ax*ax+ay*ay+az*az）;

　　ax=ax/norm;//单位化

　　ay=ay/norm;

　　az=az/norm;

　　//估计方向的重力

　　vx=2*（q1*q3-q0*q2）;

　　vy=2*（q0*q1+q2*q3）;

　　vz=q0*q0-q1*q1-q2*q2+q3*q3;

　　//错误的领域和方向传感器测量参考方向之间的交叉乘积的总和

　　ex=（ay*vz-az*vy）;

　　ey=（az*vx-ax*vz）;

　　ez=（ax*vy-ay*vx）;

　　//积分误差比例积分增益

　　exInt=exInt+ex*Ki;

　　eyInt=eyInt+ey*Ki;

　　ezInt=ezInt+ez*Ki;

　　//调整后的陀螺仪测量

　　gx=gx+Kp*ex+exInt;

　　gy=gy+Kp*ey+eyInt;

　　gz=gz+Kp*ez+ezInt;

　　//整合四元数率和正常化

　　q0=q0+（-q1*gx-q2*gy-q3*gz）*halfT;

　　q1=q1+（q0*gx+q2*gz-q3*gy）*halfT;

　　q2=q2+（q0*gy-q1*gz+q3*gx）*halfT;

　　q3=q3+（q0*gz+q1*gy-q2*gx）*halfT;

　　//正常化四元

　　norm=sqrt（q0*q0+q1*q1+q2*q2+q3*q3）;

　　q0=q0/norm;

　　q1=q1/norm;

　　q2=q2/norm;

　　q3=q3/norm;

　　Pitch=asin（-2*q1*q3+2*q0*q2）*57.3;//pitch，转换为度数

　　Roll=atan2（2*q2*q3+2*q0*q1，-2*q1*q1-2*q2*q2+1）*57.3;//rollv

　　//Yaw=atan2（2*（q1*q2+q0*q3），q0*q0+q1*q1-q2*q2-q3*q3）*57.3;//此处没有价值，注掉

　　}

　　二、一阶互补算法

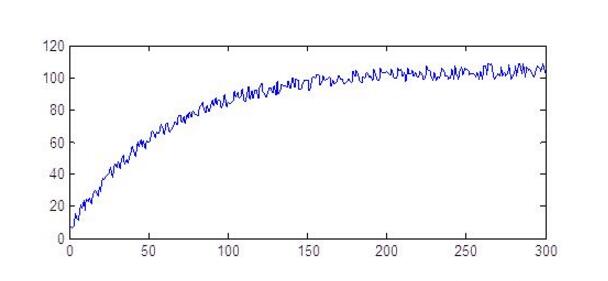
　　MPU6050可以输出三轴的加速度和角速度。通过加速度和角速度都可以得到Pitch和Roll角（加速度不能得到Yaw角），就是说有两组Pitch、Roll角，到底应该选哪组呢？别急，先分析一下。MPU6050的加速度计和陀螺仪各有优缺点，三轴的加速度值没有累积误差，且通过算tan（）可以得到倾角，但是它包含的噪声太多（因为待测物运动时会产生加速度，电机运行时振动会产生加速度等），不能直接使用；陀螺仪对外界振动影响小，精度高，通过对角速度积分可以得到倾角，但是会产生累积误差。所以，不能单独使用MPU6050的加速度计或陀螺仪来得到倾角，需要互补。一阶互补算法的思想就是给加速度和陀螺仪不同的权值，把它们结合到一起，进行修正。得到Pitch角的程序如下：

　　//一阶互补滤波

　　floatK1=0.1;//对加速度计取值的权重

　　floatdt=0.001;//注意：dt的取值为滤波器采样时间

　　floatangle;

　　angle_ax=atan（ax/az）*57.3;//加速度得到的角度

　　gy=（float）gyo［1］/7510.0;//陀螺仪得到的角速度

　　Pitch=yijiehubu（angle_ax，gy）;

　　floatyijiehubu（floatangle_m，floatgyro_m）//采集后计算的角度和角加速度

　　{

　　angle=K1*angle_m+（1-K1）*（angle+gyro_m*dt）;

　　returnangle;

　　}

　　互补算法只能得到一个倾角，这在平衡车项目中够用了，而在四轴飞行器设计中还需要Roll和Yaw，就需要两个互补算法，我是这样写的，注意变量不要搞混：

　　//一阶互补滤波

　　floatK1=0.1;//对加速度计取值的权重

　　floatdt=0.001;//注意：dt的取值为滤波器采样时间

　　floatangle_P，angle_R;

　　floatyijiehubu_P（floatangle_m，floatgyro_m）//采集后计算的角度和角加速度

　　{

　　angle_P=K1*angle_m+（1-K1）*（angle_P+gyro_m*dt）;

　　returnangle_P;

　　}

　　floatyijiehubu_R（floatangle_m，floatgyro_m）//采集后计算的角度和角加速度

　　{

　　angle_R=K1*angle_m+（1-K1）*（angle_R+gyro_m*dt）;

　　returnangle_R;

　　}

　　单靠MPU6050无法准确得到Yaw角，需要和地磁传感器结合使用。

　　三、卡尔曼滤波

　　其实卡尔曼滤波和一阶互补有些相似，输入也是一样的。卡尔曼原理以及什么5个公式等等的，我也不太懂，就不写了，感兴趣的话可以上网查。在此给出具体程序，和一阶互补算法一样，每次卡尔曼滤波只能得到一个方向的角度。

　　#include《math.h》

　　#include“stm32f10x.h”

　　#include“Kalman_Filter.h”

　　//卡尔曼滤波参数与函数

　　floatdt=0.001;//注意：dt的取值为kalman滤波器采样时间

　　floatangle，angle_dot;//角度和角速度

　　floatP［2］［2］={{1，0}，

　　{0，1}};

　　floatPdot［4］={0，0，0，0};

　　floatQ_angle=0.001，Q_gyro=0.005;//角度数据置信度，角速度数据置信度

　　floatR_angle=0.5，C_0=1;

　　floatq_bias，angle_err，PCt_0，PCt_1，E，K_0，K_1，t_0，t_1;

　　//卡尔曼滤波

　　floatKalman_Filter（floatangle_m，floatgyro_m）//angleAx和gyroGy

　　{

　　angle+=（gyro_m-q_bias）*dt;

　　angle_err=angle_m-angle;

　　Pdot［0］=Q_angle-P［0］［1］-P［1］［0］;

　　Pdot［1］=-P［1］［1］;

　　Pdot［2］=-P［1］［1］;

　　Pdot［3］=Q_gyro;

　　P［0］［0］+=Pdot［0］*dt;

　　P［0］［1］+=Pdot［1］*dt;

　　P［1］［0］+=Pdot［2］*dt;

　　P［1］［1］+=Pdot［3］*dt;

　　PCt_0=C_0*P［0］［0］;

　　PCt_1=C_0*P［1］［0］;

　　E=R_angle+C_0*PCt_0;

　　K_0=PCt_0/E;

　　K_1=PCt_1/E;

　　t_0=PCt_0;

　　t_1=C_0*P［0］［1］;

　　P［0］［0］-=K_0*t_0;

　　P［0］［1］-=K_0*t_1;

　　P［1］［0］-=K_1*t_0;

　　P［1］［1］-=K_1*t_1;

　　angle+=K_0*angle_err;//最优角度

　　q_bias+=K_1*angle_err;

　　angle_dot=gyro_m-q_bias;//最优角速度

　　returnangle；

　　}

　总结：三种融合算法都能够输出姿态角（Pitch和Roll），一次四元数法可以输出P、R、Y三个倾角，计算量比较大。一阶互补和卡尔曼滤波每次只能输出一个轴的姿态角。