1.2.1 数列极限的概念
设{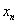 }是一个数列,a是实数,如果对于任意给定的
}是一个数列,a是实数,如果对于任意给定的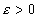 ,总存在一个正整数N,当n>N时都有
,总存在一个正整数N,当n>N时都有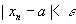 ,我们就称a是数列{
,我们就称a是数列{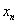 }的极限,或者称数列{
}的极限,或者称数列{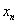 }收敛,且收敛于a,记为
}收敛,且收敛于a,记为 ,a即为
,a即为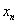 的极限。
的极限。
数列极限的几何解释: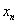 以a为极限就是对任意给定的开区间
以a为极限就是对任意给定的开区间 ,第N项以后的一切数
,第N项以后的一切数 全部落在这个区间内。
全部落在这个区间内。
1.2.2 函数极限的概念
设函数f(x)在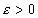 点附近(但可能除掉
点附近(但可能除掉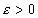 点本身)有定义,设A为一个定数,如果对任意各定
点本身)有定义,设A为一个定数,如果对任意各定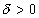 ,一定存在
,一定存在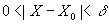 ,使得当
,使得当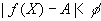 时,总有
时,总有 ,我们就称A是函数f(x)在
,我们就称A是函数f(x)在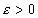 点的极限,记作
点的极限,记作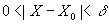 ,这时称f(x)在
,这时称f(x)在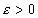 点极限存在,这里我们不要求f(x)在点
点极限存在,这里我们不要求f(x)在点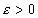 有定义,所以才有
有定义,所以才有 。
。
例如: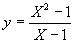 ,当x=1时,函数是没有定义的,但在x=1点函数的极限存在,显然等于2。
,当x=1时,函数是没有定义的,但在x=1点函数的极限存在,显然等于2。
1.2.3 单调有界数列必有极限
单调有界数列必有极限,是判断极限存在的重要准则之一,具体叙述如下:
如果数列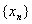 满足条件
满足条件
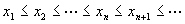 ,
,
就称数列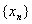 是单调增加的;反之则称为是单调减少的。
是单调增加的;反之则称为是单调减少的。
在前面的章节中曾证明:收敛的数列必有界。但也曾指出:有界的数列不一定收敛。现在这个准则表明:如果数列不仅有界,而且是单调的,则其极限必定存在。
对这一准则的直观说明是,对应与单调数列的点 只可能向一个方向移动,所以只有两种可能情形:或者
只可能向一个方向移动,所以只有两种可能情形:或者 无限趋近某一定点;或者
无限趋近某一定点;或者 沿数轴移向无穷远(因为不趋向于任何定点且递增,已符合趋向无穷的定义)。但现在数列又是有界的,这就意味着移向无穷远已经不可能,所以必有极限。
沿数轴移向无穷远(因为不趋向于任何定点且递增,已符合趋向无穷的定义)。但现在数列又是有界的,这就意味着移向无穷远已经不可能,所以必有极限。
从这一准则出发,我们得到一个重要的应用。
考虑数列 ,易证它是单调增加且有界(小于3),故可知这个数列极限存在,通常用字母e来表示它,即
,易证它是单调增加且有界(小于3),故可知这个数列极限存在,通常用字母e来表示它,即 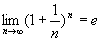 。
。
可以证明,当x取实数而趋于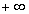 或
或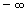 时,函数
时,函数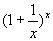 的极限存在且都等于e,这个e是无理数,它的值是 e = 2.718281828459045…
的极限存在且都等于e,这个e是无理数,它的值是 e = 2.718281828459045…
1.2.4 柯西(Cauchy)极限存在准则
我们发现,有时候收敛数列不一定是单调的,因此,单调有界数列必有极限准则只是数列收敛的充分条件,而不是必要的。当然,其中有界这一条件是必要的。下面叙述的柯西极限存在准则,它给出了数列收敛的充分必要条件。
柯西(Cauchy)极限存在准则 数列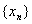 收敛的充分必要条件是:
收敛的充分必要条件是:
对于任意给定的正数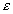 ,存在着这样的正整数N,使得当m>N,n>N时,就有
,存在着这样的正整数N,使得当m>N,n>N时,就有
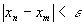 。
。
必要性的证明 设 ,若任意给定正数
,若任意给定正数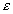 ,则
,则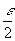 也是正数,于是由数列极限的定义,存在着正整数N,当n>N时,有
也是正数,于是由数列极限的定义,存在着正整数N,当n>N时,有 ;
;
同样,当m>N时,也有 。
。
因此,当m>N, n>N时,有
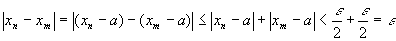
所以条件是必要的。
充分性的证明从略。
这准则的几何意义表示,数列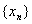 收敛的充分必要条件是:对于任意给定的正数
收敛的充分必要条件是:对于任意给定的正数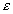 ,在数轴上一切具有足够大号码的点
,在数轴上一切具有足够大号码的点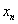 ,任意两点间的距离小于
,任意两点间的距离小于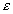 。
。
柯西极限存在准则有时也叫做柯西审敛原理。
