3.3.1 曲率的概念
来源:为了平衡曲线的弯曲程度。
平均曲率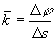 ,这个定义描述了AB曲线上的平均弯曲程度。其中
,这个定义描述了AB曲线上的平均弯曲程度。其中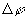 表示曲线段AB上切线变化的角度,
表示曲线段AB上切线变化的角度,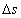 为AB弧长。
为AB弧长。
例:对于圆,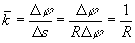 。所以:圆周的曲率为
。所以:圆周的曲率为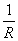 ,是常数。
,是常数。
而直线上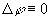 ,所以
,所以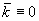 ,即直线“不弯曲”。
,即直线“不弯曲”。
对于一个点,如A点,为精确刻画此点处曲线的弯曲程度,可令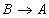 ,即定义
,即定义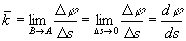 ,为了方便使用,一般令曲率为正数,即:
,为了方便使用,一般令曲率为正数,即: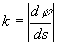 。
。
3.3.2 计算公式的推导:
由于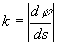 ,所以要推导
,所以要推导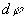 与ds的表示法,ds称为曲线弧长的微分(T5-28,P218)
与ds的表示法,ds称为曲线弧长的微分(T5-28,P218)
因为 ,所以
,所以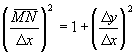 。
。
令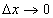 ,同时用
,同时用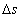 代替
代替 得
得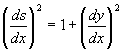
所以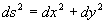 或
或
具体表示;
1、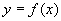 时,
时,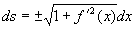
2、 时,
时,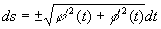
3、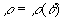 时,
时,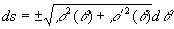 (令
(令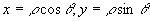 )
)
再推导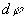 ,因为
,因为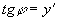 ,所以
,所以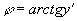 ,两边对x求导,得
,两边对x求导,得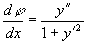 ,推出
,推出 。
。
下面将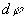 与ds代入
与ds代入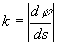 公式中:
公式中:
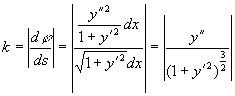 ,即为曲率的计算公式。
,即为曲率的计算公式。
3.3.3 曲率半径:
一般称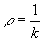 为曲线在某一点的曲率半径。
为曲线在某一点的曲率半径。
几何意义(T5-29)如图为在该点做曲线的法线(在凹的一侧),在法线上取圆心,以ρ为半径做圆,则此圆称为该点处的曲率圆。曲率圆与该点有相同的曲率,切线及一阶、两阶稻树。
应用举例:求 上任一点的曲率及曲率半径(T5-30)
上任一点的曲率及曲率半径(T5-30)
解:由于: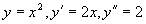
所以: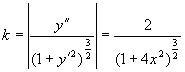 ,
,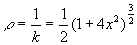
3.3.4方程的近似解法
方程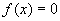 ,则
,则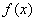 应满足:
应满足:
(1)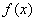 在[a,b]连续,
在[a,b]连续, 与
与 不同号。
不同号。
(2)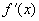 在(a,b)内连续且不变号。
在(a,b)内连续且不变号。
(3) 在(a,b)内连续且不变号。
在(a,b)内连续且不变号。
3.3.5 应用步骤:
首先:判断方程是否满足应用前提,先对端点a,b求 、
、 ,取与
,取与 同号的一点为起点。过起点做
同号的一点为起点。过起点做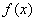 的切线,交x轴与
的切线,交x轴与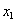 。
。
然后:过(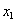 ,
,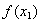 )做
)做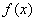 的切线,交x轴与
的切线,交x轴与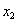 。
。
以次类推,直到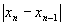 满足精度要求。
满足精度要求。
3.3.6 应用举例:
求: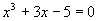 在[1,2]内的根,误差
在[1,2]内的根,误差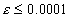
解:令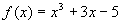 ,有:
,有:
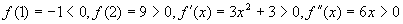
所以可应用上述方法,求得:
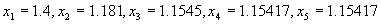
由于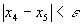 ,所以误差范围内的近似解为
,所以误差范围内的近似解为
3.3.7 两点说明:
-
前提条件的作用:
第一个条件显然是为了保证区间上解的存在性。
第二、第三个条件是为了保证各步迭代后,得到的交点仍落在区间上的
-
迭代公式: 设第n步后的交点为
 ,所以下一步过(
,所以下一步过( ,
, )做
)做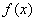 的切线,写出其方程就是:
的切线,写出其方程就是: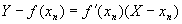 ,它与X轴交点为
,它与X轴交点为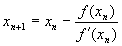 ,这就是迭代公式。
,这就是迭代公式。
