按照二重积分的定义来计算二重积分，对少数特别简单的被积函数和积分区域来说是可行的，但对一般的函数和积分区域来说，这不是一种切实可行的方法。这里介绍一种方法，把二重积分化为两次单积分（即两次定积分）来计算。
8.2.1 利用直角坐标计算二重积分
下面用几何的观点来讨论二重积分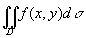
的计算问题。
在讨论中我们假定f（x，y）≥ 0。并设积分区域D可以用不等式
j 1（x）≤ y ≤ j 2（x），a≤x≤b
来表示[插图1]，其中函数j 1（x）、j 2（x）在区间 [a，b] 上连续。
插图1
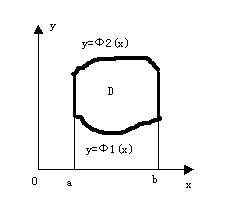
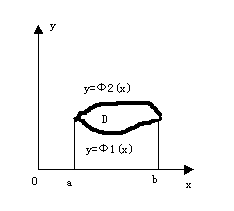
(a) (b)
插图2
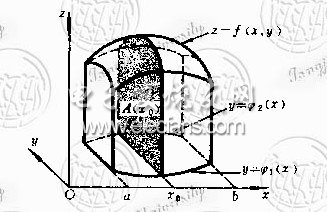
插图3
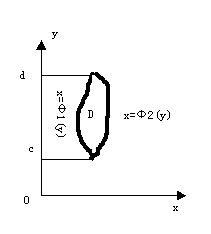
(a) (b)
插图4
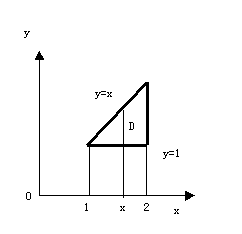
插图5
我们应用“平行截面面积为已知的立体的体积”的方法，来计算这个曲顶柱体的体积。
为计算截面面积，在区间 [a，b] 上任意取定一点x0，作平行于yOz面的平面x=x0。这平面截曲顶柱体所得截面是一个以区间 [j 1（x0），j 2（x0）] 为底、曲线z = f（x0，y）为曲边的曲边梯形（[插图2]中阴影部分），所以这截面的面积为
。
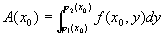一般的，过区间 [a，b] 上任一点x且平行于yOz面的平面截曲顶柱体所得截面的面积为
，
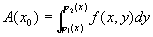于是，得曲顶柱体的体积为
。
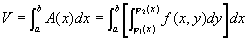这个体积也就是所求二重积分的值，从而有等式
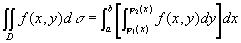。（1）
上式右端的积分叫做先对y、后对x的二次积分。就是说，先把x看作常数，把f（x，y）只看作y的函数，并对y计算从j 1（x）到j 2（x）的定积分；然后把算得的结果（是x的函数）再对x计算在区间 [a，b] 上的定积分。这个先对y、后对x的二次积分也常记作
。
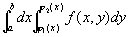因此，等式（1）也写成
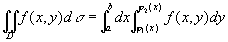，（1’）
在上述讨论中，我们假定f（x，y）≥ 0，但实际上公式（1）的成立并不受此条件限制。
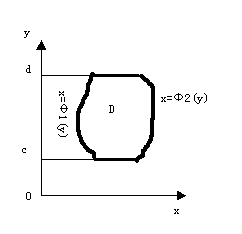
类似地，如果积分区域D可以用不等式
ψ1（y）≤ x ≤ ψ2（y），c≤y≤d
来表示[插图3]，其中函数ψ1（y）、 ψ2（y）在区间 [c，d] 上连续，那末就有
。
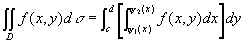上式右端的积分叫做先对x、后对y的二次积分，这个积分也常记作
。
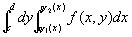因此，等式（2）也写成
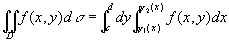，（2’）
这就是把二重积分化为先对x、后对y的二次积分的公式。
我们称图9-2-1所示的积分区域为X-型区域，图9-2-3所示的积分区域为Y-型区域。对不同的区域，可以应用不同的公式。如果积分区域D既不是X-型的，也不是Y-型的，我们可以把D分成几个部分，使每个部分是X-型区域或是Y-型区域。如果积分区域D既是X-型的，又是Y-型的，则由公式（1’）及（2’）就得
。
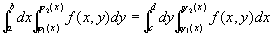上式表明，这两个不同次序的二次积分相等，因为它们都等于同一个二重积分
。
二重积分化为二次积分时，确定积分限是一个关键。而积分限是根据积分区域D的类型来确定的。
例1 计算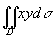
，其中D是由直线y = 1、x = 2及y = x所围成的闭区域。
解法1 首先画出积分区域D[插图4]。D是X-型的，D上的点的横坐标的变动范围是区间[1，2]。在区间[1，2]上任意取定一个x值，则D上以这个x值为横坐标的点在一段直线上，这段直线平行于y轴，该线段上点的纵坐标从y = 1变到y = x。利用公式（1）得
。
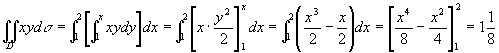解法2 把积分区域D看成是Y-型的。同学们可作为练习，验证解出的答案是否与解法1的相一致。
对于较复杂的积分区域，在化二重积分为二次积分时，为了计算简便，需要选择恰当的二次积分的次序。这时，既要考虑积分区域D的形状，又要考虑被积函数f（x，y）的特性。
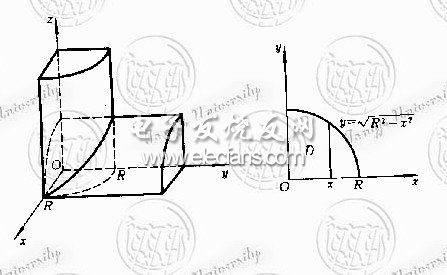
例2 求量各底圆半径都等于R的直交圆柱面所围成的立体的体积。
解 设这两个圆柱面的方程分别为
x2 + y2 = R2及x2 + z2 = R2
利用立体关于坐标平面的对称性，只要算出它在第一卦限部分[插图5]的体积V1，然后再乘以8就行了。
所求立体在第一卦限部分可以看成是一个曲顶柱体，它的底为
，
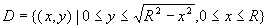如图9-2-5（b）所示。它的顶是柱面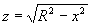
。于是，
。
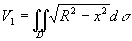利用公式（1）得
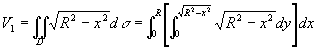
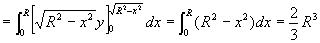
从而所求立体体积为
。
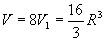8.2.2 利用极坐标计算二重积分
有些二重积分，积分区域D的边界曲线用极坐标方程来表示比较方便，且被积函数用极坐标变量r，θ比较简单。这时，我们就可以考虑利用极坐标来计算二重积分。
按二重积分的定义有
，
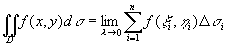下面将推导出这个和的极限在极坐标系中的形式。
假定从极点O出发且穿过闭区域D内部的射线与D的边界曲线相交不多于两点。我们用以极点为中心的一族同心圆：r=常数，以及从极点出发的一族射线：θ=常数，把D分成n个小闭区域[插图6]。
插图6
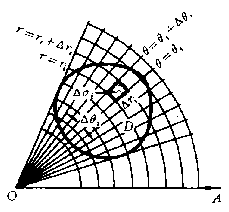
插图7
(a) (b)
插图8
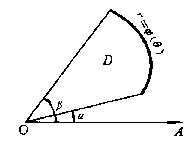
插图9
插图10
除了包含边界点的一些小闭区域外，小闭区域的面积D s i可计算如下：
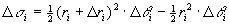
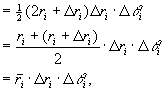
其中
表示相邻两圆弧的半径的平均值。在这小闭区域内取圆周
上的一点
，该点的直角坐标设为x i，h i，则由直角坐标与极坐标之间的关系有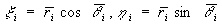
。于是
，
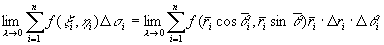即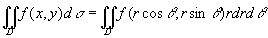 
。
由于在直角坐标系中也常记作
，所以上式又可写成
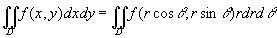。（4）
这就是二重积分的变量从直角坐标变换为极坐标的变换公式，其中rdrdθ就是极坐标系中的面积元素。
公式（4）表明，要把二重积分中的变量从直角坐标变换为极坐标，只要把被积函数中的x、y分别换成rcosθ、rsinθ，并把直角坐标系中的面积元素dxdy换成极坐标系中的面积元素rdrdθ。
极坐标系中的二重积分，同样可以化为二次积分来计算。在[插图7]，二重积分化为二次积分的公式为
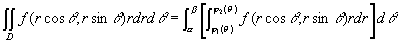。（5）
上式也写成
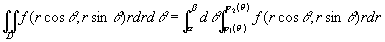。（5'）
特别地，如果积分区域D是[插图8]所示的曲边扇形，那末相当于图9-2-7（a）中φ1（θ）≡0，φ2（θ）=φ（θ）。这时闭区域D可以用不等式
0≤r≤φ（θ），α≤θ≤β
来表示，而公式（5'）成为
。
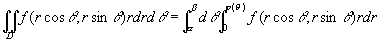如果积分区域D如图[插图9]）所示，极点在D的内部，那末相当于图9-2-8中α= 0、β= 2π。这时闭区域D可以用不等式
0≤r≤φ（θ），0≤θ≤2π
来表示，而公式（5'）成为
。
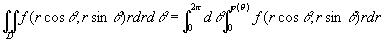由二重积分的性质4，闭区域D的面积s 可以表示为
。
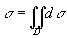在极坐标系中，面积元素ds = rdrdθ，上式成为
。
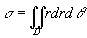如果闭区域D如图9-2-7（a）所示，这由公式（5'）有
。
特别地，如果闭区域D如图9-2-8所示，则φ1（θ）≡0，φ2（θ）=φ（θ）。于是
。
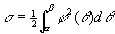例3 计算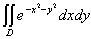
，其中D是由中心在原点、半径为a的圆周所围成的闭区域。
解 在极坐标系中，闭区域D可表示为
0≤r≤a，0≤θ≤2π。
由公式（4）及（5）有
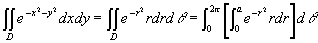
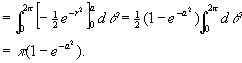
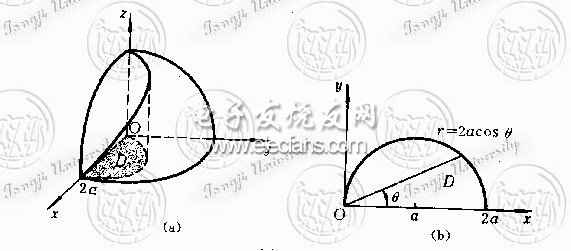
例4 求球体x2+y2+z2≤4a2圆柱面x2+y2=2ax（a>0）所截得的（含在圆柱面内的部分）立体的体积[插图10]。
解 由对称性，
，
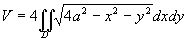其中D为半圆周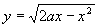
及x轴所围成的闭区域。在极坐标系中，闭区域D可用不等式
0≤r≤2acos（θ），0≤θ≤π/2
来表示。于是
。
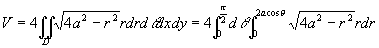
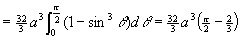