8.3 二重积分的应用实例
在二重积分的应用中，由许多求总量的问题可以用定积分的元素法来处理。如果所要计算的某个量对于闭区域D具有可加性（就是说，当闭区域D分成许多小闭区域时，所求量U相应地分成许多部分量，且U等于部分量之和），并且在闭区域D内任取一个直径很小的闭区域dσ时，相应的部分量可近似地表示为f（x，y）dσ的形式，其中（x，y）在dσ内。这个f（x，y）dσ称为所求量U的元素而记作dU，以它为被积表达式，在闭区域D上积分：
，
这就是所求量的积分表达式。
8.3.1 曲面的面积
设曲面S由方程
z = f（x，y）
给出，D为曲面S在xOy面上的投影区域，函数f（x，y）在D上具有连续偏导数fx（x，y）和fy（x，y）。我们要计算曲面S的面积A。
在闭区域D上任取一直径很小的闭区域dσ（这小闭区域的面积也记作dσ）。在dσ上取一点P（x，y），对应地曲面S上有一点M（x，y，f（x，y）），点M在xOy面上的投影即点P。点M处曲面S的切平面设为T[插图1]。
插图1
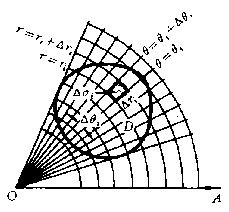
插图2
(a) (b)
插图3
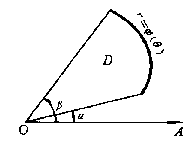
插图4
插图5
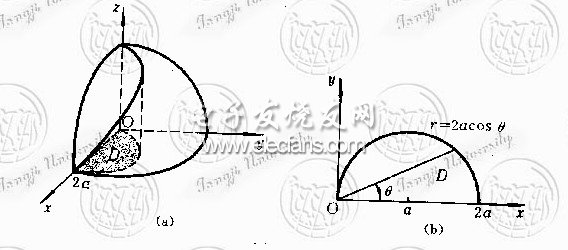
以小闭区域dσ的边界为准线作母线平行于z轴的柱面，这柱面在曲面S上截下一小片曲面，在切平面T上截下一小片平面。由于dσ的直径很小，切平面T上的那一小片平面的面积dA可以近似代替相应的那一小片面积的面积。设点M处曲面S上的法线（指向朝上）于z轴所成的角为γ，则
。
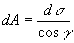因为 
，
所以 
。
这就是曲面S的面积元素，以它为被积表达式在闭区域D上积分，得
。
上式也可写为
。
这就是计算曲面面积的公式。
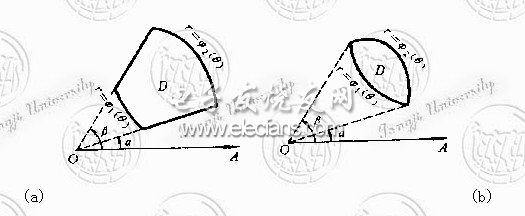
设曲面的方程为x=g（x，y）或y=h（z，x），可分别把曲面投影到xOy面上（投影区域记作Dyz）或zOx面上（投影区域记作Dzx），类似地可得
，
或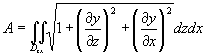
。
例1 求半径为a的球的表面积。
解：取上半球面的方程为
，则它在xOy面上的投影区域D可表示为x2+y2≤a2。
由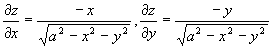 
，
得 
。
因为这函数在闭区域D上无界，我们不能直接应用曲面面积公式。所以先取区域D1：x2+y2≤b2（0<b<a）为积分区域，算出相应于D1上的球面面积A1后，令b→a取A1的极限，就得半球面的面积。
，
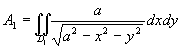利用极坐标，得
于是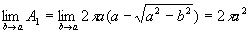 
。
这就是半个球面的面积，因此整个球面的面积为
A = 4πa2。
8.3.2 平面薄片的重心
设有一平面薄片，占有xOy面上的闭区域D，在点（x，y）处的面密度ρ（x，y），假定ρ（x，y）在D上连续。现在要找该薄片的重心的坐标。
在闭区域D上任取一直径很小的闭区域dσ（这小闭区域的面积也记作dσ），（x，y）是这小闭区域上的一个点。由于dσ的直径很小，且ρ（x，y）在D上连续，所以薄片中相应于dσ的部分的质量近似等于ρ（x，y）dσ，这部分质量可近似看作集中在点（x，y）上，于是可写出静矩元素dMy及dMx：
dMy = xρ（x，y）dσ，dMx =yρ（x，y）dσ。
以这些元素为被积表达式，在闭区域D上积分，便得
。
又由第一节知道，薄片的质量为
。
所以，薄片的重心的坐标为
。
如果薄片是均匀的，即面密度为常量，则上式中可把ρ提到积分记号外面并从分子、分母中约去，这样便得均匀薄片重心的坐标为
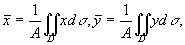（1）
其中
为闭区域D的面积。这时薄片的重心完全由闭区域D的形状所决定。我们把均匀平面薄片的重心叫做这平面薄片所占的平面图形的形心。因此，平面图形D的形心，就可用公式（1）计算。
例2 求位于两圆r = 2sinθ和r = 4sinθ之间的均匀薄片的重心[插图2]
解 因为闭区域D对称于y轴，所以重心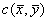
必位于y轴上，于是
。
再按公式
计算
。由于闭区域D位于半径为1与半径为2的两圆之间，所以它的面积等于这两个圆的面积之差，即A = 3π。再利用极坐标计算积分：
。
因此
，
所求重心是C（0，7/3）。
三、平面薄片的转动惯量
设有一薄片，占有xOy面上的闭区域D，在点（x，y）处的面密度ρ（x，y），假定ρ（x，y）在D上连续。现在要求该薄片对于x轴的转动惯量Ix以及对于y轴的转动惯量Iy。
应用元素法，在闭区域D上任取一直径很小的闭区域dσ（这小闭区域的面积也记作dσ），（x，y）是这小闭区域上的一个点。由于dσ的直径很小，且ρ（x，y）在D上连续，所以薄片中相应于dσ的部分的质量近似等于ρ（x，y）dσ，这部分质量可近似看作集中在点（x，y）上，于是可写出薄片对于x轴以及对于y轴的转动惯量元素：
dIx = y2ρ（x，y）dσ,dIy = x2ρ（x，y）dσ。
以这些元素为被积表达式，在闭区域D上积分，便得
。
例3 求半径为a的均匀半圆薄片（面密度为常量ρ）对于其直径边的转动惯量。
解：取坐标系如图[插图3]所示，则薄片所占闭区域D可表示为
x2+y2≤a2，y≥0；
而所求转动惯量即半圆薄片对于x轴的转动惯量Ix。
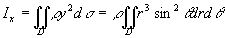
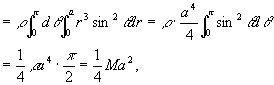
其中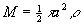
为半圆薄片的质量。