8.4.1 利用柱面坐标计算三重积分
设M（x，y，z）为空间内一点，并设点M在xOy面上的投影P的极坐标为r，θ，则这样的三个数r，θ，z就叫做点M的柱面坐标[插图1]，
插图1
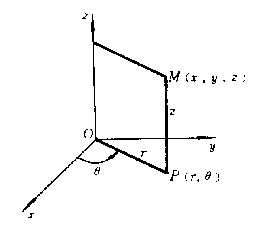
插图2
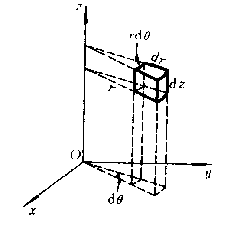
插图3
插图4
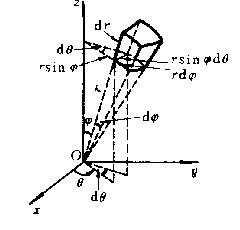
插图5
这里规定r、θ、z的变化范围为：
0 ≤ r < +∞,
0 ≤θ≤ 2π,
-∞ < z < +∞。
三组坐标面分别为
r = 常数，即以z轴为轴的圆柱面；
θ=常数，即过z轴的半平面；
z = 常数，即与xOy面平行的平面。
显然，点M的直角坐标与柱面坐标的关系为
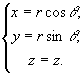（1）
现在要把三重积分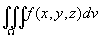
中的变量变换为柱面坐标。为此，用三组坐标面r = 常数，θ=常数，z = 常数把Ω分成许多小闭区域，除了含Ω的边界的一些不规则小闭区域外，这种小闭区域都是柱体。考虑由r，θ，z各取得微小增量dr，dθ，dz所成的柱体的体积[插图2]。柱体的高为dz、底面积在不计高阶无穷小时为r dr dθ（即极坐标系中的面积元素），于是得
dv = r dr dθdz，
这就是柱面坐标中的体积元素。再注意到关系式（1），就有
（2）
其中F（r，θ，z）= f（r cosθ，r sinθ，z）。（2）式就是把三重积分的变量从直角坐标变换为柱面坐标的公式。至于变量变换为柱面坐标后的三重积分的计算，则可化为三次积分来进行。化为三次积分时，积分限是根据r，θ，z在积分区域Ω中的变化范围来确定的，下面通过例子来说明。
例1 利用柱面坐标计算三重积分
，其中Ω是由曲面z = x2+y2与平面z = 4所围成的闭区域。
解 把闭区域Ω投影到xOy面上，得半径为2的圆形闭区域D：0≤r≤2，0≤θ≤2π。在D内任取一点（r，θ），过此点作平行于z轴的直线，此直线通过曲面z = x2+y2穿入Ω内，然后通过平面z = 4穿出Ω外。因此闭区域Ω可用不等式
r2≤z≤4，0≤r≤2，0≤θ≤2π
来表示。于是
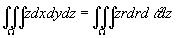
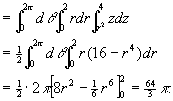
8.4.2 利用球面坐标计算三重积分
设M（x，y，z）为空间内一点，则点M也可用这样三个有次序的数r，φ，θ来确定，其中r为原点O与点M间的距离，φ为有向线段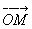
与z轴正向所夹的角，θ为从正z轴来看自x轴按逆时针方向转到有向线段
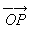的角，这里P为点M在xOy面上的投影[插图3]。这样的三个数r，φ，θ叫做点M的球面坐标，这里r，φ，θ的变化范围为
0 ≤ r < +∞,
0 ≤φ≤ π,
0 ≤θ≤ 2π.
r = 常数，即以原点为心的球面；
φ= 常数，即以原点为顶点、z轴为轴的圆锥面；
θ = 常数，即过z轴的半平面。
点M的直角坐标与球面坐标的关系为
（3）
为了把三重积分中的变量从直角坐标变换为球面坐标，用三组坐标面r = 常数，φ=常数，θ= 常数把积分区域Ω分成许多小闭区域。考虑由r，φ，θ各取得微小增量dr，dφ，dθ所成的六面体的体积[插图4]。不计高阶无穷小，可把这个六面体看作长方体，其经线方向的长为rdφ，纬线方向的宽为r sinφdθ，向径方向的高为dr，于是得
dv = r 2 sinφdrdφdθ，
这就是球面坐标系中的体积元素。再注意到关系式（3），就有
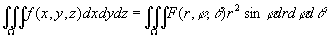,（4）
其中F（r，φ，θ）= f（r sinφcosθ，r sinφsinθ，r cosφ）。（4）式就是把三重积分的变量从直角坐标变换为球面坐标的公式。
要计算变量变换为球面坐标后的三重积分，可把它化为对r对φ及对θ的三次积分。
若积分区域Ω的边界曲面是一个包围原点在内的闭曲面，其球面坐标方程为r = r（φ，θ），则
。
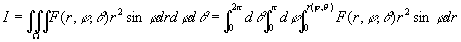当积分区域Ω为球面r = a所围成时，则
。
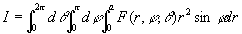特别地，当F（r，φ，θ）= 1时，由上式即得球的体积
，
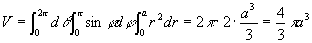这是我们所熟知的。
例2 求半径为a的球面与半顶角为α的内接锥面所围成的立体[插图5]的体积。
解 设球面通过原点O，球心在z轴上，又内接锥面的顶点在原点O，其轴与z轴重合，则球面方程为r = 2acosφ，锥面方程为φ=α。因为立体所占有的空间闭区域Ω可用不等式
0≤r≤2acosφ, 0≤φ≤α, 0≤θ≤2π
来表示，所以
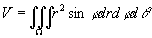
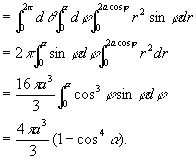
在三重积分的应用中也可采用元素法。
设物体占有空间闭区域Ω，在点（x，y，z）处的密度为ρ（x，y，z），假定这函数在Ω上连续，求该物体的重心的坐标和转动惯量。与第三节中关于平面薄片的这类问题一样，应用元素法可写出
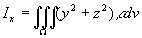
等，其中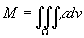
为物体的质量。
例3 求均匀半球体的重心。
解 取半球体的对称轴为z轴，原点取在球心上，又设球半径为a，则半球体所占空间闭区域Ω可用不等式
x2+y2+z2≤a2，z≥0
来表示。
显然，重心在z轴上，故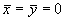
。
，
其中
为半球体的体积。
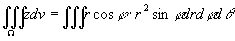
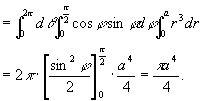
因此，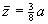
，重心为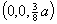
。