9.1 曲线积分
9.1.1 第一类曲线积分
公式: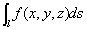 =
=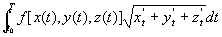
应用前提:
1.曲线L光滑,方程可以写成为: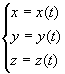
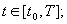
2.函数 在L上有定义,且连续。
在L上有定义,且连续。
公式变形:若L为平面曲线,L方程为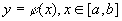 ,则公式可以写成为:
,则公式可以写成为:
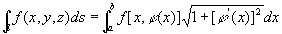
常用计算法:
1.对于曲线L可以写成为参数形式的,可直接套用公式.
2.对于平面曲线,可以用公式的变形.
3.计算中,根据图形特点,直接将ds化为dx,dy或dz.
如: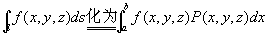 ,其中:ds=P(x,y,z)dx ,x
,其中:ds=P(x,y,z)dx ,x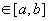
4.当L是简单的折线段时,可以将L分为几个连续线段的和,然后分别求积分,再求和。(注意:由于折线段不连续,所以这种情况下不能对L直接套用公式,否则,公式中的 将有无意义的点.
将有无意义的点.
公式推导及证明
推导的总体思想:将曲线L先分割,再求和,最后取极限。推导过程中要用到:中值定理,弧长公式及连续函数的一些极限性质.
分割:在L上插入n个分割点,令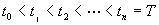 ,(
,(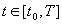 );
);
记d=max(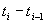 ),
),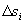 为[
为[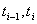 ]上的弧长,
]上的弧长,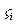 为[
为[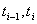 ]上任意一点.
]上任意一点.
求和:利用积分定义,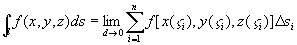
由弧长公式: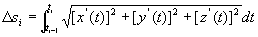
由中值定理: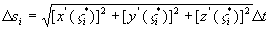
其中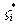 是由中值定理确定的[
是由中值定理确定的[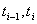 ]上的一点,
]上的一点, ;
;
于是: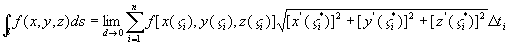
利用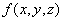 ,
,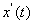 ,
,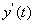 ,
,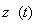 的连续性,有:
的连续性,有:
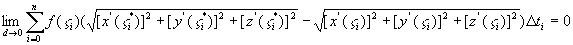 于是:
于是: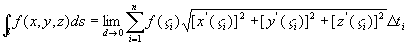
右端是黎曼积分和数,利用黎曼积分定义
取极限:得公式:
9.1.2 第二类曲线积分
问题的来源:物理上,力F作用于物体上,使之沿曲线AB由A运动到B,求力F所做的功W.
公式的推导
分割:将AB曲线分为小弧段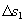 ,
,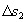 ,...,
,...,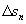 .在每个小段上将F视为常力F
.在每个小段上将F视为常力F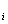 .于是
.于是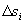 上作功
上作功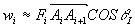 ,(其中,
,(其中,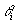 是
是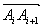 线段与
线段与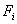 的夹角)
的夹角)
设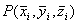 ,
, ,
,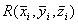 是
是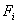 在x,y,z三轴正方向的投影.
在x,y,z三轴正方向的投影.
则: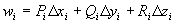
做和: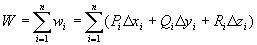
9.1.3 两类曲线积分的联系
设曲线上以(t,x),(t,y),(t,z)表示正向切线t与三正向坐标系的夹角.于是
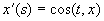 ,
,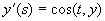 ,
, ,据二类曲线计算公式:
,据二类曲线计算公式:
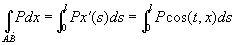 ;
;
由一类曲线推导得: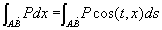
由曲线方程对称性的公式如下:
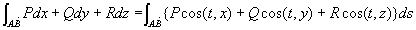
对于平面时,公式可化为:
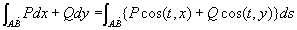
平面上,设n为法方向,t为切向,则cos(t,x)=cos(n,y),cos(t,y)=-cos(n,x)
于是: