9.2.1 第一类曲面积分
思想:与曲线积分类似,只不过分割的是平面.曲线积分中一切线段代替曲线段,
这里以微小切平面代替曲面.接下来是求和,取极限.
公式: 其中z=f(x,y)为曲面方程.也可写成
其中z=f(x,y)为曲面方程.也可写成
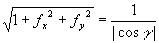 ,其中
,其中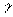 为法线与z轴夹角.
为法线与z轴夹角.
若s为参数形式x=x(u,v),y=y(u,v),z=z(u,v)由于
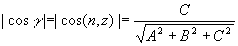 ,
,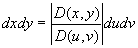
(其中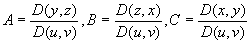
所以公式可化为

若记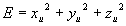 ,
,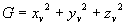 ,
,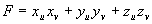
则公式亦可写为: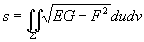 .
.
计算方法:
1.利用原始公式求积分.(但是注意:有些方程虽不能写成
z=z(x,y)的显示形式,但利用隐式求导.求出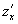 与
与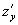 后.
后.
由于方程的特殊形式,有可能消去子项,从而可利用原始
公式.
2.化方程为参数方程.计算A,B,C或E,F,G利用推倒公式
求积分.
3.有些方程利用图像的对称性.可以只求其中的几个部
分即可.这样做可大大降地计算量.
公式推广:
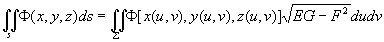
第一式中z=f(x,y).第二式E,F,G定义同上.
9.2.2 第二类区面积分
同第二类曲线积分的推导及形式,相类似的有积分形式为:
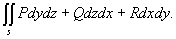
下面求第二类曲面的计算公式: 与上述推导类似,分割,做和,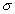 与I
与I
相比较,有

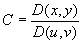
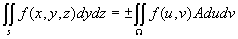
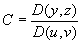
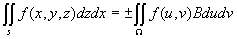
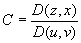
对于正负号的取舍,适当uv平面的正向与曲面s选定一侧相
关的正向相互对应时取正号,否则取负.
因为第二类区面积分计算可利用上述公式将
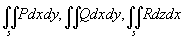 分别计算,然后求和.
分别计算,然后求和.
