9.3.1 两类曲面积分的联系
对于微小面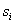
有
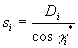(由中值定理得其存在性).作和
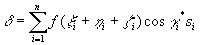,由于
.
取极限: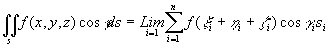
,
其中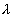
为微小元
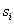的直径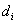
的最大值.因为
,
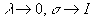于是得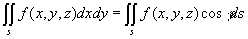
由方程对称性得到联系方程
(
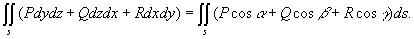
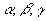为法线与x,y,z轴的夹角)
9.3.2 格林(Green)公式:
,
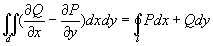其中:l为光滑曲线,D为平面单连通区域,l为D的边界. P,Q在D及l上连续,并且有对x,y的连续偏导,右侧积分取区域正向,即延正向前进,区域在左边.
9.3.3 高斯(Gauss)公式:
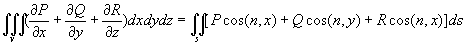
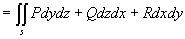
其中:s为光滑曲面.V为空间单连通区域,s为V的边界. P,Q,R在V及s上对x,y,z有连续偏导数, N为s外法线方向,最后的积分是延区面s的外侧.
9.3.4 斯托克斯(Stokes)公式:
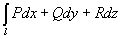
其中:l为光滑曲线s为光滑曲面. L为s的边界. P,Q,R在s及l上对x,y,z有连续偏导数,曲线积分方向与曲面的侧依右手定则联系.